Joule

This post presents general material about SI ( Système International [d’Unités]), created by the Bureau international des poids et mesures. It started out as a presentation of the joule in particular. In addition, a number of personal prejudices about units of measurement are freely presented.

What appeals to me about SI is that fact that it is a system, not an arbitrary collection of units. Its units are the only ones with official metric status since 1960.

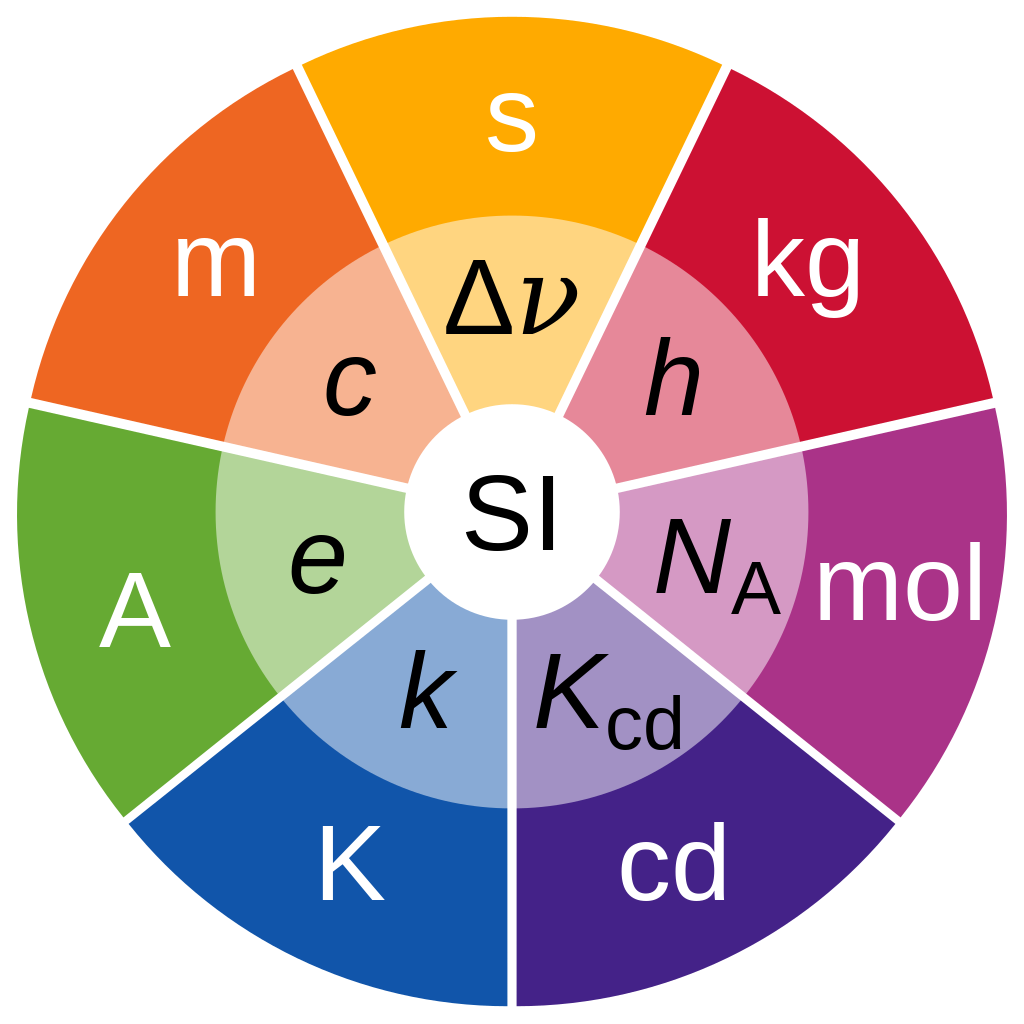
There are seven base units: the second (symbol s, the unit of time), metre (m, length), kilogram (kg, mass), ampere (A, electric current), kelvin (K, thermodynamic temperature), mole (mol, amount of substance), and candela (cd, luminous intensity). The system allows for an unlimited number of coherent derived units, which can always be represented as products of powers of the base units. Twenty-two coherent derived units have special names and symbols. It may not be perfect, but it is consistent, which makes it easy to use.

Since 2019, the magnitudes of all SI units have used seven defining constants to express their values. These are: the speed of light in vacuum c, the hyperfine transition frequency of caesium Δν_Cs, the Planck constant h, the elementary charge e, the Boltzmann constant k, the Avogadro constant N_A, and the luminous efficacy K_cd.

For most of my life, I have been trying to forget the number of feet or yards in a mile. I can’t. Yet, I cannot easily express a mile in inches. I would have to take one of those numbers I am struggling to forget, and multiply it by either 12 or 36, respectively. In contrast, there is no problem converting metric units. 1 km = 1 000 m = 1 000 000 mm.

If anyone wonders why I use a space as a separator, it is because both a comma (,) and a period/ point (.) are used to indicate the start of decimal fractions. Most of the time I use a period/ point (as is the preference in English speaking countries), while most continental Europeans, including Norwegians, use a comma. Yes, I am capable of using a comma, if required. The keys are right beside each other on my computer keyboard. On paper, the symbol I use deliberately looks like something in between – an elongated period/ point, or a truncated comma.

The so-called Imperial system is not international. In terms of liquid measure the system employs four units: 4 gills = 1 pint; 2 pints = 1 quart; 4 quarts = 1 gallon. In the American system a gallon is 3.785 litres or 231 cublic inches. This American system deviates in several areas from the one Brexiters are wanting to reimpose in England, and the one I grew up with in Canada. Here, a gallon is 4.54609 litres or 277.4194 cubic inches. The Imperial system of units was first defined in the British Weights and Measures Act 1824. It continued to be developed through a series of Weights and Measures Acts and amendments.

Of course, this only applies to liquids. Dry materials have their own system where one starting point is the dry gallon. The US fluid gallon is about 14.1% smaller than the dry gallon, while the Imperial fluid gallon is about 3.2% larger. The system involves: 2 pints = 1 quart; 4 quarts = 1 dry gallon; 2 dry gallons = 1 peck; 4 pecks = 1 bushel; 10 pecks or 2.5 bushels = 1 barrel.

For me, dry units of volume were just something to memorize. It was not until a librarian from Wisconsin described the basket I was using to transport grass clippings from a lawn to a compost heap, as a bushel basket, that I began to understand the size of that unit. Thank you, Jane.

Imperial measurements of length are equally convoluted. Here are some, and their relationship to a foot, a unit that is precisely defined as 0.3048 m. A twip = 1/ 17 280; a thou or mil = 1/ 12 000; a barleycorn = 1/ 36; an inch = 1/ 12; a hand = 1/ 3; a yard = 3; a rod = 16.5; a chain = 66; a furlong = 660; a mile = 5 280.

In surveying, much of the emphasis is in determining area, typically the acre, in the Anglosphere. Here the rod is particularly useful: 4 rods = 1 chain; 40 rods = 10 chains = 1 furlong. Whole number multiples of a rod can be used to determine area in acres. A perfect acre is 40 rods by 4 rods or 160 square rods or 10 square chains. To gain a rough understanding of area in units that I understand, I take the area in acres and divide it by 250. This gives an approximate area in square kilometers. In metric units, a prevalent standard unit of area is the hectare, which is 100 m by 100 m = 10 000 square meters. There are 100 hectares in one square kilometer.

At sea, other measurements are used that are subdivisions of the nautical mile (n.m.) = 1 852 meters. These are fathom = 1/ 1 000 n.m. = 1.852 m = 6.0761 feet (and not 6 feet, as myth would have it, although the British Admiralty allowed – some would say encouraged – this deviation); cable = 100 fathoms = 1/ 10 of a nautical mile = 185.2 m.

In the seamanship and navigation courses I have taken in Norway, a nautical mile is used extensively. In 1 degree (°) of latitude or longitude = 60 minutes (‘). 1′ = 60 seconds (“). While distances vary along parallels of latitude, that run east to west, the distances are constant along meridians of longitude that run north to south: 1’ = 1 n.m. and 1° = 60 n.m.

In an interconnected world, there is a need for a common language of measurements. Take speed, as an example. While your local meteorologist uses m/s, your local Harley-Davidson motorcyclists may be using miles/hour (refusing to use km/h, even in Europe). 1 m/s = 3.6 km/hour, exactly = about 2.237 miles per hour. Most people cannot judge speeds precisely, but rely on instruments – including speedometers – to tell them. Thus, it should be possible to set up some approximations that could help with transitions.

I survived a speed limit transition in Canada, 1977-09-01, when motor vehicle speed limits went from mph to km/h. My (imperfect) recollection of the speeds were: 10 mph = 20 km/h; 20 mph = 30 km/h; 30 mph = 50 km/h; 40 mph = 60 km/h; 50 mph = 80 km/h; 70 mph = 110 km/h. Those with better memories can contact me, and these will be corrected. The highest speed limit in Canada is 120 km/h found on British Columbia’s Coquihalla Highway.

At the time there were complaints that 30 mph was actually only 48.28 km/h. However, it was also pointed out that the average Canadian driver drove at speeds that exceeded the speed limit. It was judged more appropriate to use round numbers. The opposite problem arose with 20 mph = ca. 32.19 km/h while the new speed limit was only 30 km/h.

In terms of accident prevention, speeds in m/s gives relevant information to drivers, who know that they have to react to events within seconds. While a speed of 10 km/h is about 2.78 m/s, it can be regarded as 3 m/s. With this approach, speed limits become: 10 mph = 20 km/h = 6 m/s; 20 mph = 30 km/h = 9 or more likely 10 m/s; 30 mph = 50 km/h = 15 m/s; 40 mph = 60 km/h = 18 or more likely 20 m/s; 50 mph = 80 km/h = probably 25 m/s; 70 mph = 110 km/h = 30 m/s.

The Bureau international des poids et mesures (BIPM) is an intergovernmental organisation, with 63 member-states and 40 associate states/ economies, that sets measurement standards in four areas: chemistry, ionising radiation, physical metrology, and coordinated universal time. It is based in Saint-Cloud, on international territory located in a suburb almost 10 km west of Paris, France. It was founded 1875-05-20. This date continues to be celebrated annually as World Metrology Day.

There have been many proposals for metric base units. The first was developed by Carl Friederich Gauss (1777 – 1855), who proposed using millimetre, milligram and second in 1832. In 1873, a British Association for the Advancement of Science committee that included both James Clerk Maxwell (1831 – 1879) and William Thomson (1824 – 1907) recommended centimetre, gram and second. This became known as the cgs system, and was officially adopted in 1881. In 1881, Rudolf Clausius (1822 – 1888) proposed erg as the official energy unit, from ergon = work/ task in Greek. It was officially adopted in 1882, but lost its official status on 1978-01-01.

Wilhelm Siemens (1823 – 1883) proposed joule as a unit in 1882, to honour James Prescott Joule (1818 – 1889) for his work in thermodynamics. Originally, it was defined in terms of amperes and ohms. This tended to make it an electrical unit. However, in 1946 it was redefined in terms of newtons and meters, to make it a more generalized and acceptable unit of work. In 1948, the joule became the preferred unit of heat, effectively replacing the calorie. It can always be defined in terms of base units: kg⋅m²⋅s⁻²

The problem with calories. First, there are two different types of calories: large calories or kilocalories = 1 000 small calories or gram calories. These are related to the energy needed to raise either 1 kilogram or 1 gram of water, respectively, 1 Celsius = 1 Kelvin. The small calorie was included in the SI system, but it was replaced by the joule in 1948. 1 small calorie = 4.184 J; 1 large calorie = 1 kilocalorie = 4.184 kJ. These can most easily be expressed as 4 J or 4 kJ, respectively.

Adding to the confusion, there are also watt-hours. The international unit of time is the second. 1 Wh (watt-hour) = 60 x 60 = 3 600 Ws (watt-seconds) = 3.6 kWs, which is just another name for a joule. So, 1 Ws = 1J.

The size of rechargeable batteries is increasingly expressed in terms of electric charge (Ah). I regard this as a marketing ploy to increase the apparent energy capacity of a battery. People want to know how long a battery will last before it has to be recharged. The electric charge in itself is uninteresting, because it has to be multiplied by the voltage used. This varies. I have computers that use 10.8 V, radios that use 13.8 V, electric power tools that use 18 V, a lawnmower that uses 40 V. Most of the time there is a caveat on the battery, stating that this is the maximum voltage.

The 40 V electric lawnmower battery I held in my hand a few seconds ago is rated at 5.0 Ah. It also states that it provides 180 Wh of energy, not the 200 that should be expected by multiplying 5 x 40. Part of the reason for my skepticism about using Ah as a metric, is that it does not take voltage drop into account. Internal resistance, and chemical transformations in the electrolyte are two reasons for this decline in voltage. Regardless, I expect battery manufacturers to provide me with realistic values for the amount of energy I can use, before charging.

For traction batteries used in electric vehicles, kWh is the common unit, in part because many people do not know (or even care about) the battery voltage. On modern vehicles this can vary from 200 to 800 V.

What I hope is that electric battery suppliers will provide energy values in joules. The 180 Wh in the lawnmower battery noted above is 648 MJ. This is about the size of the smallest battery pack used in a scooter. The smallest battery pack for a car is currently about 20 kWh traction battery offers 72 GJ; 40 kWh = 144 GJ; 60 kWh = 216 GJ; 80 kWh = 288 GJ; 100 kWh = 360 GJ. A battery pack for a locomotive might be 2 400 kWh. However, I would appreciate more standardized batteries using preferred numbers, as developed by Charles Renard (1847–1905). If the R5 were implemented it would lead to traction batteries of 630 MJ, 1 GJ, 2.5 GJ, 4.0 GJ, 6.3 GJ, 10 GJ, 16 GJ, 25 GJ, 40 GJ, 63 GJ, 100 GJ, 160 GJ, 250 GJ, 400 GJ, 630 GJ, 1.0 TJ, 1.6 TJ, 2.5 TJ, 4.0 TJ, 6.3 TJ and 10 TJ for assorted vehicle types, covering everything from scooters to locomotives.

Metabolism refers to necessary processes to keep a body functioning. Standard metabolic rate (SMR) is the rate of energy expenditure per unit time by animals at rest. Basal metabolic rate (BMR) is a special case of SMR used with endothermic aka warm-blooded animals. In humans, BMR is the amount of energy per unit of time that a person needs to keep the body functioning at rest: breathing, blood circulation, controlling body temperature, cell growth, brain and nerve function, and contracting muscles. BMR accounts for about 60 to 75% of an individual’s energy expenditure. There are suggestions that a mean BMR could be somewhat over 6 MJ per day.

It is often suggested that the average human consumes about 2 000 – 2 500 large calories of food per day, in round numbers. This is somewhere around 8 – 10 MJ per day, in yet more round numbers.

For joules to be understood in kitchens and the heads of people on diets, there will also be a need to internalize values. On one website, a list of 45 common food products was presented, along with the calories of each. One of these was a banana, medium which offered 105 calories. Bananas vary in size, and I am uncertain exactly how big a medium banana is. I am sure that I have eaten small bananas that provide only 80 calories, and larger ones that have 120. Thus, I am going to state that on at least some days, my banana only has 100 calories. Since 1 large calorie has about 4 kJ, this item will provide me with 400 kJ of energy. I do not see using joules, instead of calories, as an insurmountable challenge.

On a personal note: One Norwegian has been director of the Bureau, Ole Jacob Broch (1818 – 1889), from 1883 (some sources say 1879) until his death. At various times he was a mathematician, physicist, economist and government minister. He was born in Fredrikstad, Norway, from where I trace my Norwegian ancestry. The spelling of his surname is precisely how Norwegians want to spell my forename, unless they know better.

Related, future posts. Prolog, provides information about the Prolog programming language. Cooksum, examines metabolism, “the sum of the physical and chemical processes in an organism by which its material substance is produced, maintained, and destroyed, and by which energy is made available.” In particular it looks at the work of Herman Pontzer. The content of these four posts, will be used in Cookbase, a nutritional knowledge base being developed as a kitchen tool. It builds, a database of ingredients and their characteristics, recipes with number of servings, ingredients and quantities, preparation instructions etc.